SlowStom
Funding: Laboratory of Excellence Advanced Research on the Biology of Tree and Forest Ecosystems (ARBRE; grant ANR-11-LABX-0002-01) and Université de Lorraine.
Partners: Groups FARE and ForeSTree of Silva (INRAE Nancy). Coordinated by Emilie Joetzjer (ForeSTree).
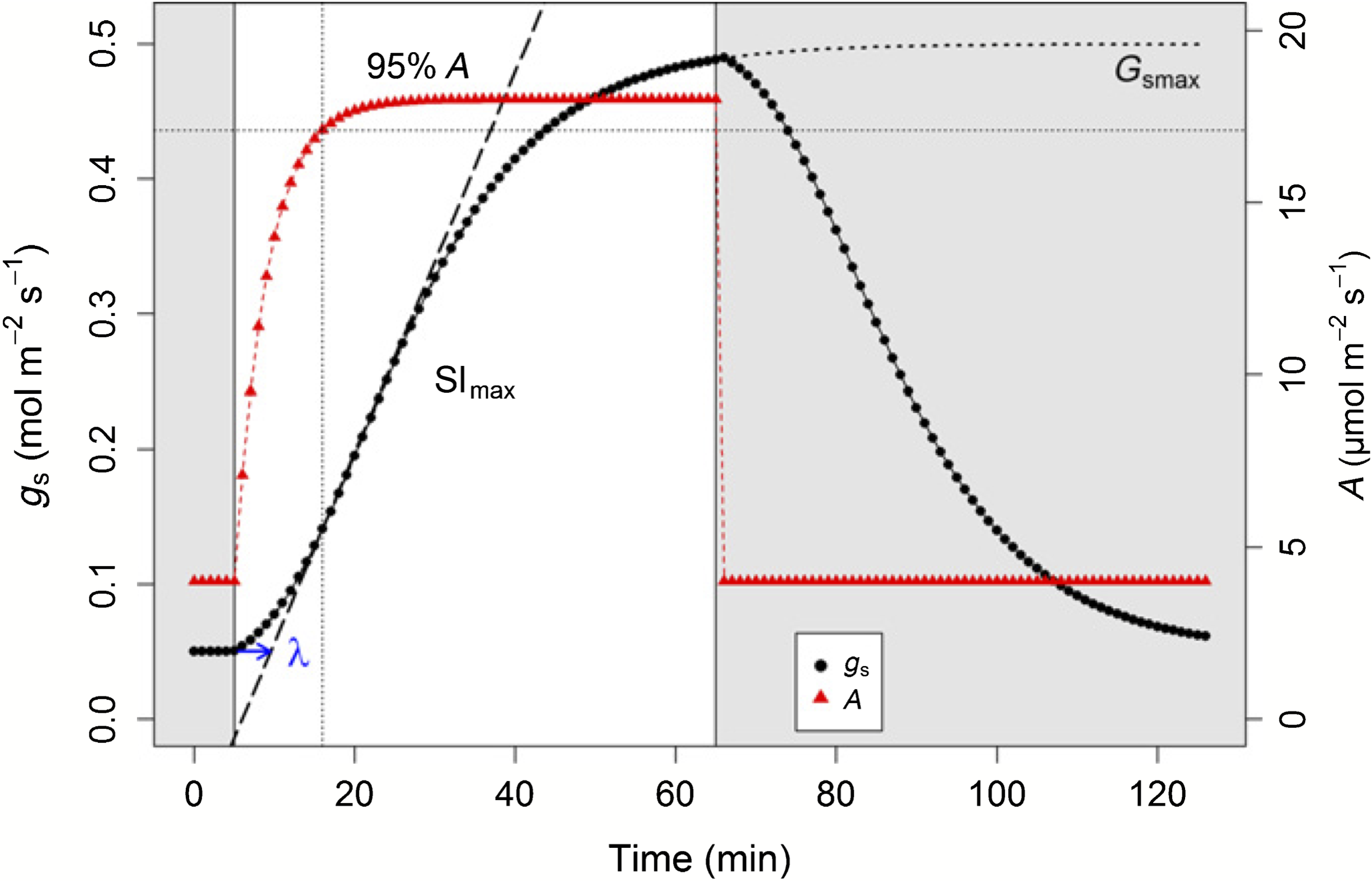
Plants constantly adapt photosynthesis and stomatal conductance to prevailing environmental conditions. Photosynthesis can adjust in seconds to changes in irradiance while stomatal conductance responds lagged by a few minutes up to almost an hour. There is a fundamental difference between shade flecks (sudden decrease in irradiance) and sun flecks (sudden increase of irradiance). In the former case, stomata are open, CO2 is (mostly) not limiting, and photosynthesis can immediately respond to the drop in irradiance. In the latter case, stomata are more closed, limiting the supply of CO2 to photosynthesis so that it also shows a lagged response to increased irradiance, even though still faster than stomatal conductance (cf. figure on title page). This manoeuvre between coupled and uncoupled situations happens continuously on partly overcast days with intermittent light conditions.
Hence, the questions on ecosystem scale about this well-known phenomenon on leaf scale are:
- Can uncoupled photosynthesis and stomatal conductance of the canopy due to sun/shade flecks be detected on ecosystem scale?
- Are there situations with uncoupled canopy photosynthesis and canopy conductance for example on partly overcast days?
Ecosystem models use coupled descriptions of photosynthesis and stomatal conductance. They use so-called steady-state descriptions for stomatal and canopy conductance. It was shown that these steady-state descriptions cannot fully comprehend the behaviour of photosynthesis and stomata in intermittent light conditions but that non-steady-state descriptions of stomatal conductance are needed during these unsteady times. Almost all ecosystem models also calculate with fixed modelling time steps, which are mostly given by the time resolution of the flux observations and the meteorological forcing data. Model parameters are hence adapted for mean conditions during the model time step, which theoretically should be different during stable and intermittent meteorological conditions.
Questions for the description of canopy conductance in ecosystem models arise:
- How big is the influence of non-steady state descriptions of canopy conductance on ecosystem fluxes of H2O and CO2 in ecosystem models?
- Do dynamic descriptions of canopy conductance improve estimates of mean ecosystem fluxes of half an hour under stable and intermittent meteorological conditions compared to steady-state descriptions using adaptive time stepping?
- Is it possible to use closed integral forms of non-steady state canopy conductance with a fixed time stepping in ecosystem models to calculate ecosystem fluxes in different meteorological conditions?
These questions lead to the specific objectives of this project:
- Use Fourier analysis (spectrograms) of high-frequency data of eddy covariance (20 Hz) to analyse maximum time scales of contributing turbulent eddies to observed eddy covariances.
- Use continuous wavelet transforms to calculate ecosystem fluxes with one-minute resolution.
- Use high-frequency meteorologic data (20 s) together with the one-minute ecosystem fluxes for the calculation of canopy conductance.
- Use coupled neural networks on the calculated ecosystem fluxes to derive canopy photosynthesis with one-minute resolution.
- Use irradiance to classify stable and intermittent meteorological conditions.
- Analyse the coupling of photosynthesis and canopy conductance under different meteorological conditions.
- Implement transient and integral formulations of non-steady-state stomatal conductance in the ecosystem model MuSICA.
- Analyse the performance of different descriptions of stomatal conductance and different time stepping schemes on ecosystem fluxes under diverse meteorological conditions.
Objectives 1, 3, 4, 6, 7, and 8 have never been tackled before and extend current data processing and analysis of eddy covariance data.